Les graphes
Bibliographie
Ce résumé de cours est basé essentiellement sur le
DIU - EIL
22 mars 2021
Paul Sabatier Toulouse
Représentation d'un graphe
Un peu de vocabulaire
Un graphe non orienté est un couple ( X , E ) où X est un ensemble fini de sommets et E un ensemble de paires { x, y } de deux éléments de X appelées arêtes.
Un graphe orienté est un couple ( X , E ) où X est un ensemble fini de sommets et E un ensemble de couples ( x, y ) d'éléments de X appelées arcs.
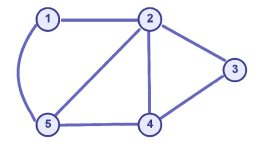
G 1 = { X = {1, 2, 3, 4, 5},E = {{1, 5}, {2, 1}, {2, 4}, {3, 2}, {4, 3}, {5, 2}, {5, 4}}}
noter l'utilisation d'accolades
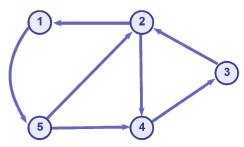
G 2 = { X = {1, 2, 3, 4, 5},E = {(1, 5), (2, 1), (2, 4), (3, 2), (4, 3), (5, 2), (5, 4)}}
noter l'utilisation de parenthèses dans ce cas
On peut également utiliser la représentation sagittale , elle n'est pas unique , sur cet exemple , 8 sommets et 12 arêtes.
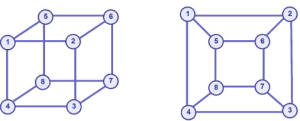
Représentation par matrice d'adjacence
Exemple : Pour un graphe non orienté
Avec deux exemples, cela doit-être suffisant pour la compréhension ..
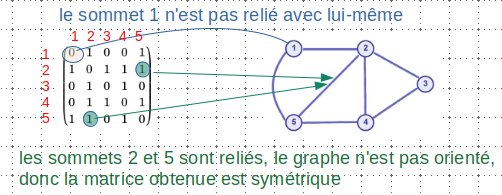
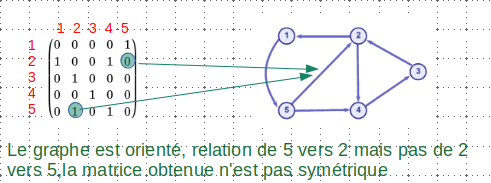
Représentation par les listes d'adjacence
Exemple : Encore deux exemples : orienté et non orienté
En python, on parlerai de liste de liste pour cette représentation .., remarquer la notation entre crochets
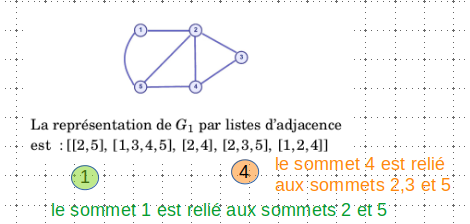
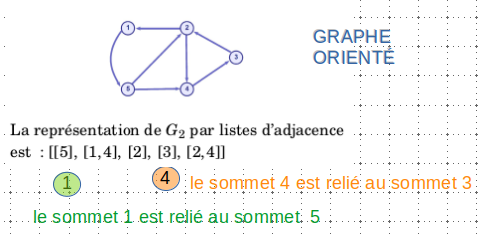
Parcourir un graphe
Pourquoi ?
Une application bien connue des graphes est par exemple de trouver le plus court chemin entre deux points (application par exemple) aux échanges de données entre réseau informatiques.
On peut facilement élargir la notion de "plus court chemin" à :
plus long / rapide en temps
plus ou moins cher en coût (péages)
Dans ce cas, on parle de graphes pondérés
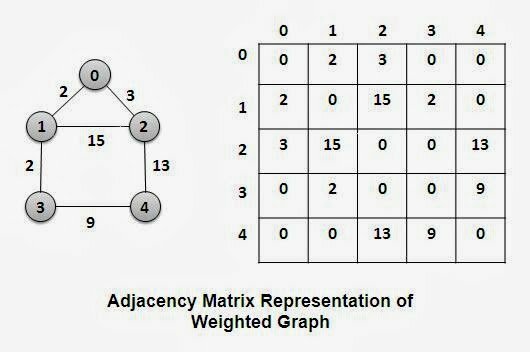
Par exemple, dans ce cas, il y a un coût à chaque liaison, et on peut chercher le moins 'cher', pour aller de 0 à 4 :
0 -> 2 -> 4 : coût 16
0->1->3->4 : coût 13
On utilise généralement deux types de parcours de graphe .
Parcours en largeur
Définition : Méthode
Le parcours en largeur est un parcours "prudent". On part d'un sommet X, on commence par visiter tous les voisins de X , puis les voisins des voisins et ainsi de suite
Exemple : Un exemple
Retrouver le ressource complète ici :
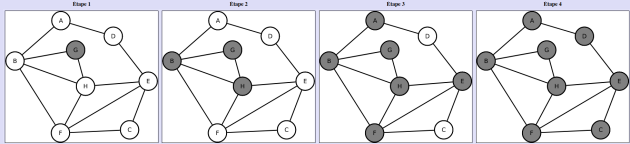
En partant du sommet G, étape par étape, on grise au fur et a mesures les sommets visités et on propose le résultat sous forme de liste en python :
[G,B,H,A,F,E,D,C]
Parcours en profondeur
Définition : Méthode
Le parcours en profondeur consiste, à partir d'un sommet donné, à suivre un chemin le plus loin possible, sans passer deux fois par le même sommet. Quand on rencontre un sommet déjà visité, on fait marche arrière pour revenir au sommet précédent et explorer les chemins ignorés précédemment.
Exemple : Exemple
Si on l'exemple précédent , un parcours possible serait en partant de G :
[G,H,F,C,E,D,A,B]
Programmation autour d'un graphe
Comment définir un graphe et l'utiliser dans un programme
En python, on utilisera un dictionnaire avec une liste d'adjacence
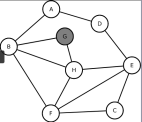
M={
"A":{"B","D"},
"B":{"A","F","G","H"},
"C":{"E","F"},
"D":{"A","E"},
"E":{"C","D","F","H"},
"F":{"B","C","E","H"},
"G":{"B","H"},
"H":{"B","E","F","G"}
}
Attention : Quelles fonctions utiliser ?
Comme tous les langages utilisés, python dispose d'un grand nombre fonctions , il faut bien faire attention à celles que l'on autorise ou pas !
Cela va dépendre des connaissances que et savoir faire que l'on désire tester.
le nombre de sommets
Fonctions dictionnaires autorisées
Ici, autorise uniquement le parcours par clefs /valeurs
ledico = {'a':0,'b':1,'c':2,'d':3,'e':4,'d':5}#parcours clefs/valeurs
for key, value in ledico.items():
print (key, value)
#parcours par clefs
for key in ledico:
print (key)
Exemple : En utilisant uniquement parcours par clefs/valeurs ou par clefs , écrire une fonction nbs qui prenne en argument un dictionnaire et retourne le nombre de sommets
Compléter le listing ci-dessous :
M={"A":["B","D"],
"B":["A","F","G","H"],
"C":["E","F"],
"D":["A","E"],
"E":["C","D","F","H"],
"F":["B","C","E","H"],
"G":["B","H"],
"H":["B","E","F","G"]
}
Exemple : Recherche du nombre d'arêtes
En utilisant uniquement :
parcours par clefs/valeurs ou par clefs ,
En utilisant la fonction len(L) qui donne la longueur d'une liste
écrire une fonction nba qui prenne en argument un dictionnaire et retourne le nombre d'arêtes, le graphe est non orienté et présenté sous forme d'un dictionnaire ou chaque clef est un sommet et sa valeur la liste au sens python des sommets adjacents.
M={"A":["B","D"],
"B":["A","F","G","H"],
"C":["E","F"],
"D":["A","E"],
"E":["C","D","F","H"],
"F":["B","C","E","H"],
"G":["B","H"],
"H":["B","E","F","G"]
}
Exemple : De la définition par liste d'adjacence à la matrice d'adjacence.
On part toujours du même graphe M, écrire la fonction ToMatrice qui prend en argument le dictionnaire M et retourne la matrice d'adjacence A en partant du code ci-dessous
La matrice d'adjacence doit être affichée proprement .
M={"A":["B","D"],"B":["A","F","G","H"],
"C":["E","F"],
"D":["A","E"],
"E":["C","D","F","H"],
"F":["B","C","E","H"],
"G":["B","H"],
"H":["B","E","F","G"]
}
taille = len(M)
def pos(Lettre):
Liste = ["A","B","C","D","E","F","G","H"]
return Liste.index(Lettre)
def CreeMatriceCarree(m):
M = []
for i in range(m):
L = []
for j in range(m):
L.append(0)
M.append(L)
return M
def AfficheMatriceCarre(Mat):
for Elt in Mat :
for i in range(len(Mat)):
print(Elt[i],end=" ")
print()
AfficheMatriceCarre(CreeMatriceCarree(taille))
def CreeMatriceCarree(m):
M = []
for i in range(m):
L = []
for j in range(m):
L.append(0)
M.append(L)
return M
def AfficheMatriceCarre(Mat):
for Elt in Mat :
for i in range(len(Mat)):
print(Elt[i],end=" ")
print()
AfficheMatriceCarre(CreeMatriceCarree(taille))
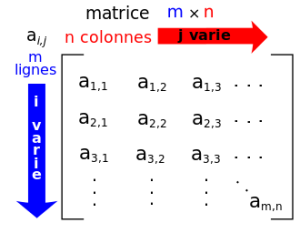
Exemple structure d'une matrice